跳到主要内容

sin36°的手工计算

· 阅读需 2 分钟

之前看到一篇文章（见此），其中有说道sin36°的计算。

自己尝试了下，果真不会算。

其实不会算的原因在于没有画好图，而且参考了错误的思路。

下面演示下正确的计算方法：​

草稿纸开始作图（如下图）

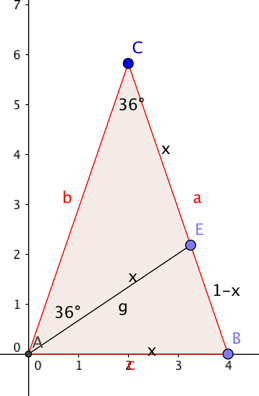
  • 画一个等腰三角形ABC，角C为36°。则角A角B均为72°。（三角形内角180°）
  • 画角A的角平分线，相交CB于E点。此时角EAB为36°。角AEB为72°。

通过以上两步，我们发现：

  • 我们有了三个等腰三角形。CAB和ECA和ABE。
  • 三角形相似，则对应边成比例。（来源于相似三角形公式）

image

下面，我们开始进行计算。​

假设CB长度为1，此时CE=AE=AB为x。EB则为1-x。

相似三角形，底边比斜边相等：

BEAB=ABCB\frac{BE}{AB} = \frac{AB}{CB}

即：

1−xx=x1\frac{1-x}{x} = \frac{x}{1}

x2=1−xx^2 = 1-x

对结果进行整理：

x2+x−1=0x^2 +x-1= 0

使用求根公式：

x=−b±b2−4ac2ax=\frac{-b\pm\sqrt{b^2-4ac}}{2a}

带入后得到：

x=−1±12+42=−1±52x=\frac{-1\pm\sqrt{1^2+4}}{2}=\frac{-1\pm\sqrt{5}}{2}

在这里，显然是x>0的。所以：

x=−1+52x=\frac{-1+\sqrt{5}}{2}

好。基本上每条线的长度我们都是已知的了。此时要求sin36°，可以转化为求角CAE的正弦。​

我们再做一条辅助线：

  • 做E点的垂直线，相交CA于垂足D。

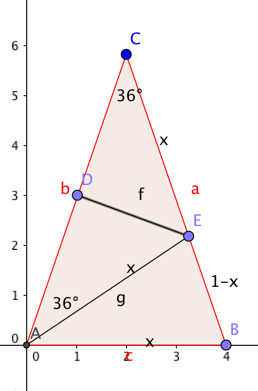
image

这样就有：

sin36o=DEAE=AE2−AD2AEsin36^o = \frac{DE}{AE}=\frac{\sqrt{AE^2-AD^2}}{AE}

sin36o=x2−0.52xsin36^o=\frac{\sqrt{x^2-0.5^2}}{x}

sin36o=(−1+52)2−0.52−1+52sin36^o = \frac{\sqrt{(\frac{-1+\sqrt{5}}{2})^2-0.5^2}}{\frac{-1+\sqrt{5}}{2}}

sin36o=(6−254)−14−1+52sin36^o =\frac{\sqrt{(\frac{6-2\sqrt{5}}{4})-\frac{1}{4}}}{\frac{-1+\sqrt{5}}{2}}

sin36o=5−254−1+52sin36^o =\frac{\sqrt{\frac{5-2\sqrt{5}}{4}}}{\frac{-1+\sqrt{5}}{2}}

sin36o=125−25−1+52sin36^o =\frac{\frac{1}{2}\sqrt{5-2\sqrt{5}}}{\frac{-1+\sqrt{5}}{2}}

sin36o=5−25−1+5sin36^o =\frac{\sqrt{5-2\sqrt{5}}}{-1+\sqrt{5}}

sin36o=5−25∗(5+1)2(5−1)(5+1)sin36^o =\frac{\sqrt{5-2\sqrt{5}}*\sqrt{(\sqrt{5}+1)^2}}{(\sqrt{5}-1)(\sqrt{5}+1)}

sin36o=5−25∗(5+1+25)4sin36^o =\frac{\sqrt{5-2\sqrt{5}}*\sqrt{(5+1+2\sqrt{5})}}{4}

sin36o=(5−25)∗(6+25)4sin36^o =\frac{\sqrt{(5-2\sqrt{5})}*\sqrt{(6+2\sqrt{5})}}{4}

sin36o=10−254sin36^o =\frac{\sqrt{10-2\sqrt{5}}}{4}

最终检验​

sqrt(10-2*sqrt(5))/4

ans = 0.58779

sin(36/180*pi)

ans = 0.58779

计算正确。